This file type includes high-resolution graphics and schematics when applicable.
While 5G standards are still very much evolving, the goals for higher data rates, lower-latency network accesses, and more energy-efficient implementations are clear. And with higher data rates comes the need for wider bandwidth spectrums. Today, available bandwidth in the spectrum up through 6 GHz isn’t sufficient to satisfy these requirements. This, in turn, has helped move the target operating frequency bands up into the millimeter-wave range for the next generation of wireless communication systems.
The small wavelengths at these higher frequency bands enable implementations with many more antenna elements per system within very small form factors. However, it also increases the signal-path and propagation challenges associated with operating at these frequencies. For example, the attenuation due to gas absorption for a 60-GHz waveform is more than 10 dB/km, while a 700-MHz waveform experiences an attenuation on the order of 0.01 dB/km.
These losses can be offset with intelligent array design and the use of spatial signal-processing techniques, including beamforming. This type of processing is enabled by large arrays and can be used directly to provide higher link-level gains to overcome path loss and undesirable interference sources.
To achieve the most control and flexibility with beamforming in an active array design, it’s desirable to have independent weighting control over each antenna-array element. This requires a transmit/receive (T/R) module dedicated to each element. For array sizes typical of a large multiple-input, multiple-output (MIMO) communication system (e.g., over a thousand elements), such an architecture is difficult to build due to cost, space, and power limitations.
For example, implementing a very high performance analog-to-digital converter (ADC) and digital-to-analog converter (DAC) for every channel (along with the supporting components) can drive the cost and power beyond allocated design budgets. Similarly, having variable gain amplifiers in the RF chain for each channel increases system cost.
Going Hybrid
Hybrid beamforming is a popular technique that can be used to partition beamforming between the digital and RF domains. System designers can implement hybrid beamforming to balance flexibility and cost tradeoffs while still fielding a system that meets the required performance parameters.
Hybrid-beamforming designs are developed by combining multiple array elements into subarray modules. A T/R module can be dedicated to multiple elements in the array; thus, the system will require fewer T/R modules. The number of elements in each subarray can be selected to ensure that system-level performance is met across the range of steering angles.
Using the transmit path as an example, each element within a subarray can have a phase shift applied directly in the RF domain, while digital beamforming techniques based on complex weighting vectors can be applied on the signals that feed each subarray. Digital beamforming allows for control of the signal for both amplitude and phase on signals aggregated at the subarray level. For cost and complexity reasons, the RF control is typically limited to applying phase shifts to each of the elements.
Systems such as the one shown in Figure 1 are complex to develop. Modeling techniques can be used to design and evaluate large antenna arrays and the corresponding RF and digital architectures needed to help manage their complexity. These techniques help reduce risk and validate design approaches at the earliest stages of a project. In addition, it’s important to evaluate subsystem designs in the context of the larger system. For example, how will hybrid beamforming tradeoffs affect the bit error rate on communications with a mobile device?
Designing the Array
The first step in the design process is to model and design the array. This includes converging on array design choices such as the array geometry, element spacing, the lattice structure of the elements, and tapering. In addition, the effects of mutual coupling are important to characterize before implementing the final design. Once an initial configuration of the array design is complete, architectural partitioning can be iteratively evaluated against the overall system performance.
With millimeter-wave systems, the area is reduced in proportion to the wavelength size. As an example, an antenna array designed at millimeter-wave frequencies can be up to 100 times smaller than an array designed to operate at microwave frequencies. By building an array with a larger number of antenna elements, we can achieve a high beamforming gain. The highly directive beam helps offset the increased path loss at higher frequencies of operation, as beams are steered to a specific direction.
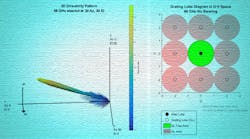
To achieve steering in azimuth and elevation, a uniformly spaced planar array in the y and z plane can be designed. Figure 2 shows an example of a 64×64 uniform rectangular array. The larger number of elements provides a high level of directivity. The design also has tapering applied to the rows and columns of the array to reduce sidelobe levels.
As is the case with all design choices, the larger antenna gains achieved with narrower beams must be balanced with the fact that MIMO systems are based on scattering environments. These environments also depend on broader beam patterns to maximize channel capacity. This tradeoff can be assessed as part of the modeling, too.
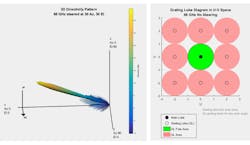
The image on the right side of Figure 2 shows that with spacing of wavelength/2 between the elements, no grating lobes are present across the full range of steering directions, as expected. It’s important to understand the impacts here, because it may be necessary to increase the spacing between the elements to mitigate the effects of mutual coupling. This crucial design consideration must be accounted for at this juncture.
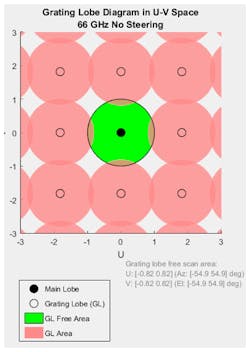
Fortunately, at the higher frequencies, where wavelength/2 spacing is quite small to start with, an increase in element separation by 10% of a wavelength only requires a change of less than 0.5 mm at 66 GHz. Figure 3 shows the tradeoff that must be considered when using a grating lobe diagram with a 10% increase in the spacing between the elements. For this example, grating lobes are only present with azimuth and elevation angles outside ±54.9 degrees.
Extending the Model Fidelity
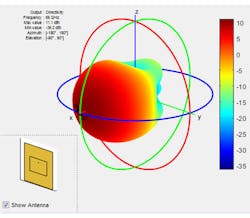
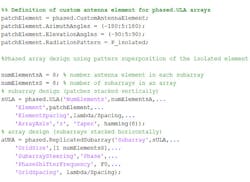
Next, in a more detailed example, an array is built up as a collection of subarrays. The element used in this example, which is based on a patch antenna designed for 66-GHz resonance, is no longer ideal. The element pattern for a single patch element is shown in Figure 4.
To build up an array using this pattern, each subarray is modeled as an 8×1 element uniform linear array, where each element has a pattern response from the patch element. Eight subarrays are then replicated to form an 8×8 array as shown in the MATLAB code below.
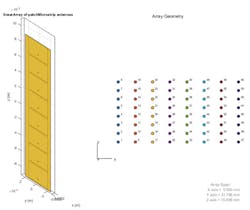
The resulting array structure can be visualized like that shown in Figure 5, with each subarray (8 elements × 1 subarray) on the left and the full array (1 subarray replicated in 8 columns) on the right.
From the hybrid-beamforming perspective, each of the elements within the 8×1 array can be passed through a phase shifter for steering in the elevation plane. We see how this can be modeled in the RF domain with the phase shifters in the following section. Each of the eight signals that feed the subarrays can be controlled via digital beamforming techniques to steer the beam in azimuth.
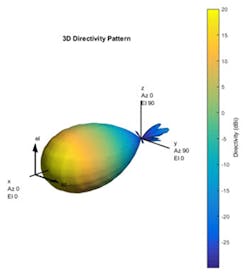
Figure 6 shows the resulting beam pattern for the array in the above configuration, which has been calculated using superposition.
Hybrid-Beamformer Partitioning
We can then partition the architecture for the transmit chain with the phase shifts (applied in the RF domain) and complex weights (applied in the digital domain). For basic analysis, the weights are able to be generated using MathWorks’ MATLAB, Phased Array System Toolbox, and Antenna Toolbox code, as shown in the code below:
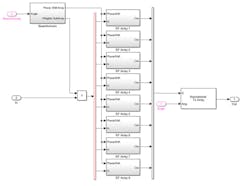
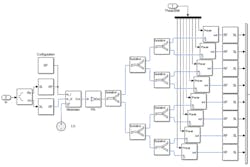
Applying the array design parameters, the digital weights and the RF phase shifts generated in MATLAB earlier (a multi-domain simulation) can be performed using the architecture model in Simulink (Fig. 7). In this block diagram, the phase shifts are provided as inputs to each of the subarrays, which are then applied to the RF signals. The digital beamforming weights are used to shape the signals feeding each of the subarrays.
Figure 8 provides a detailed view into a single RF Array block from Fig. 7. The RF phase shifters shown in Fig. 8 perform the beamforming in the elevation plane, while the baseband weights provide the beamforming in the azimuth plane.
Multi-Beam Hybrid System Architectures
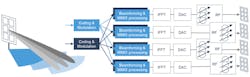
The model can be extended to support multi-user beamforming systems. To do this, the baseband beamforming blocks described above are employed to create multiple beams from the array to cover multiple users concurrently (Fig. 9). This beamforming can also be used to account for the path variations between the transmitter and the desired user locations.
The resulting signals are able to be combined to perform the RF beamforming and serve the different users in a sector at specific distances from the base station. As discussed earlier, the subarray modules enable coarse elevation angle adjustment (by phase shifters), and multi-user groups can be arranged by distance in a ring structure to effectively provide areas of coverage.
Summary
By implementing a hybrid-beamforming system, designers can strike a balance between meeting system performance goals and system-level cost objectives.
Developing a hybrid beamformer and evaluating algorithm alternatives is only the first step toward achieving the required performance of a wireless communications system. To assess performance, the beamformer must be integrated into a system-level model and evaluated over a collection of parameter, steering, and channel combinations.
Modeling these beamforming algorithms in the context of an entire system, including RF, antenna, and signal-processing components, can help verify design choices at the earliest phases of the project and reduce the associated challenges.